コレクション 直角 三角形 三 平方 の 定理 324752-直角三角形 三平方の定理 覚え方

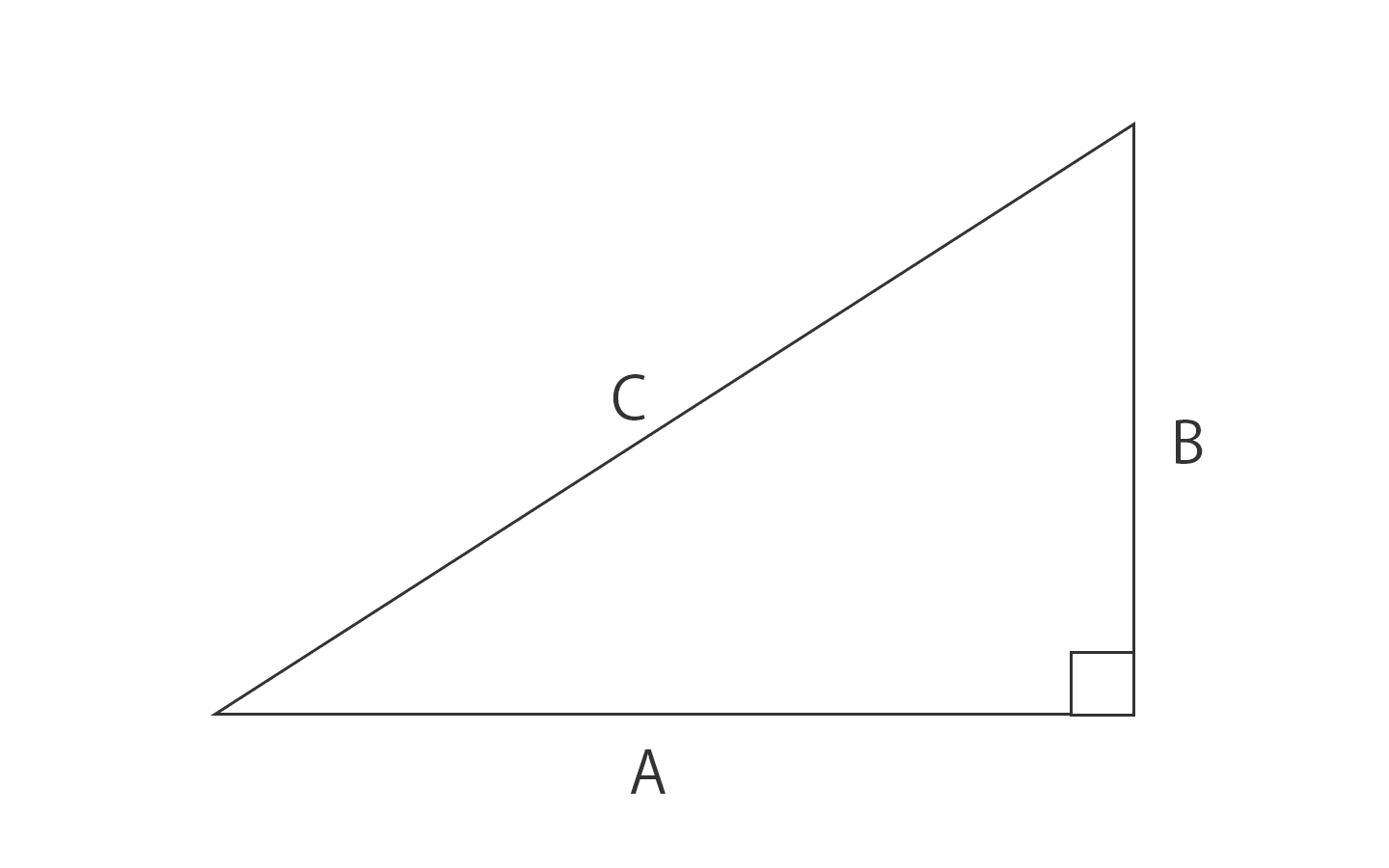
三平方の定理 例題 三平方の定理 三平方の定理2 三平方_平行四辺形の対角線 特別な直角三角形_補助線が必要な問題 二等辺三角形の面積 台形の面積 三平方_三辺の長さから三角形の面積を求める 三平方_座標平面の三角形 三平方_座標(最短距離) 三平方_座標(点と直線の距離) 三平方_折り返し立体の表面積展開図（入試問題） → 携帯版は別頁 《解説》 次のような直角三角形の三辺の長さについては， a 2b 2=c 2 が成り立ちます．（これを三平方の定理といいます．） 逆に，三辺の長さについて， a 2b 2=c 2 が成り立つとき，その三角形は直角直角三角形で、3つの辺の長さが全て整数になる場合はどのような場合でしょうか？ 実は、3つの辺の長さを a 、 b 、 c とすると、 直角三角形になる a 2 b 2 = c 2 となることが知られています。 （中学数学で習うピタゴラスの定理から分かります） 例えば

中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su

直角三角形 三平方の定理 覚え方

直角三角形 三平方の定理 覚え方- これらの形を暗記すると、よりスピーディに計算できるようになります。 もちろん、万が一それぞれの辺の比を忘れてしまっても、直角三角形の \(2\) 辺の長さがわかっていれば、もう \(1\) 辺の長さは三平方の定理で導き出せるので、あわてないでくださいね。三平方の定理とは、直角三角形の3辺の長さの関係を表す公式の事を言います。 また、別名「ピタゴラスの定理」とも呼ばれています。 この呼び方の方が有名でしょうか。 古代中国でもこの定理は使われていて、それが日本に伝わり、江戸時代には鉤股弦

三平方の定理 自動計算サイト

タレスの定理（タレスのていり、英 Thales' theorem ）とは、直径に対する円周角は直角である、つまり、A, B, C が円周上の相異なる 3 点で、線分 AC が直径であるとき、∠ABC が直角であるという定理である。 ターレスの定理、タレースの定理ともいう。 歴史 古代ギリシャの哲学者、数学者タレス三平方の定理（ピタゴラスの定理）と公式の証明忍者が用いた三角の知恵 が成り立つことを、 三平方の定理 と言います。 三平方の定理は、別名「ピタゴラスの定理」とも言います。 例えば、直角をはさむ2つの辺の長さが 3 c m と 4 c m の直角三角形三角定規型 暗記しておくべき直角三角形があります。 それは三角定規の形です。 三角定規は \(2\) 種類あります。 その \(2\) 種類は必ず暗記すべき特別な直角三角形です。 45° 45° 90° まずはじめに直角

ただし， ∣ a b c ∣ abc ∣ a bc ∣ で三角形 a b c abc a bc の面積を表します。 三平方の定理の三次元空間バージョンです！ なお，四平方の定理というと整数論におけるラグランジュの四平方和定理（→整数論の美しい定理7つの5つ目）のことを指す場合もあるので注意して下さい。 精选优质文档倾情为你奉上 第二讲 直角三角形 要点梳理 要点一勾股定理 直角三角形两直角边的平方和等于斜边的平方如果直角三角形的两直角边长分别为，斜边长为，那么 要点诠释： 1勾股定理揭示了一个直角三角形三边之间的数量关系 2利用勾股,文客久久 三平方の定理というと, 直角三角形において, (斜辺の2乗) = (他の2辺の2乗の和) が成り立つという有名な定理です ここでは, 三平方の定理 (平面上の定理)を3次元に拡張した, 四平方の定理を紹介します 定理 3つの面が直角三角形で, 1つの頂点に直角が集まっ

 三平方の定理を使って直角三角形の辺の長さを求める4つの問題 三平方の定理をつかった問題でよく出てくるのは、 直角三角形の辺の長さを求める問題。 今日はこの問題を4つのパターンに分けてみたぞ。 超基本タイプ;三平方の定理を使うと、直角三角形の 2 つの辺の長さからもう一つの辺の長さを求めることができます。 このページでは、三平方の定理を分かりやすく説明しています。中学校で学習する前の人にも、三平方の定理の意味を理解してもらえるような解説にしているので、ぜひお読みください。 ピタゴラスの定理とは、古代ギリシアの数学者で哲学者のピタゴラスが立ち上げた団体が発見した数学の定理のこと。直角三角形をなす3辺のうち、2辺の長さを知ることができれば、残り1辺の長さを知ることができるというものです。 公式：a² b² = c²

直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典

見本pdf 新中学問題集 発展編 塾用教材 教育開発出版株式会社 Scm H S3 Mihon

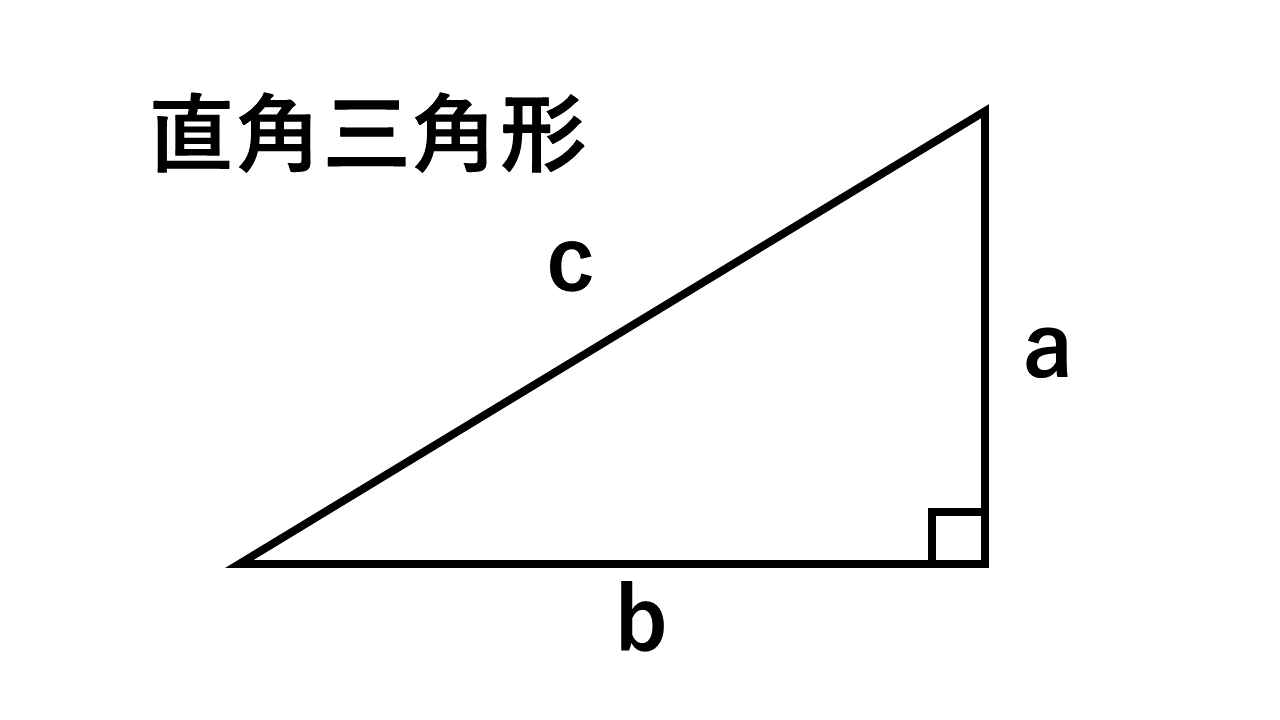
ピタゴラスの定理の覚え方としては、 斜辺の平方は他の2辺の平方の和 が最も優れているだろう。 昨今の生徒の意識として、結果さえ覚えればOKで、その成り立ち等に関心を払わない 場合が多い。三平方の定理の解説 直角三角形における3辺の長さによる定理を 三平方の定理 (さんへいほうのていり)と言います。 ピタゴラスの定理とも言われます。 三平方の定理では、直角三角形の斜辺をc、その他の辺をそれぞれa、bとした場合に、 a 2 b 2 = c 2 が成り立ちます。 この三平方の定理（ピタゴラスの定理）とは何かっていうと、 直角三角形の3つの辺の関係を表した公式 なんだ。 もうちょっと具体的にいうと、直角三角形には、 斜辺の2乗は、直角をはさむ辺を2乗して足したものと等しい っていう関係があるんだ

三平方の定理 やややさしい数学

中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su

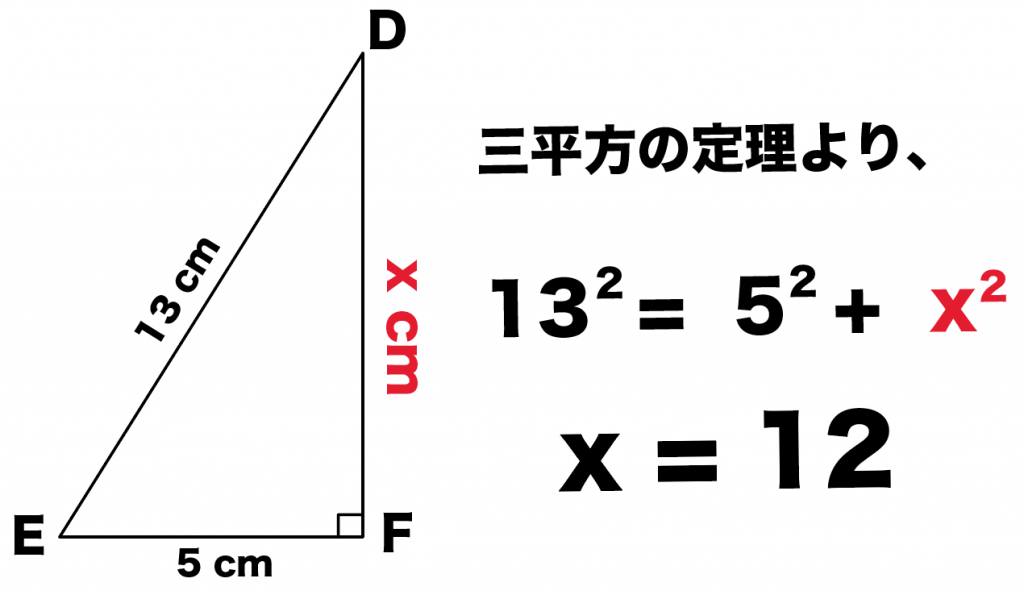
では直角三角形を図にしていきましょう。 sinは高さ/斜辺 なので、直角三角形の 高さ5,斜辺13 とわかります。 底辺は、 三平方の定理 を使えば、 a 2 b 2 =c 2 5 2 底辺 2 =13 2 底辺=12 とわかります。 ヘロンの公式の図解 Step① 内接円の性質から S = s r Step② s − a, s − b, s − c を見つける Step③ A P ′ = s を示す Step④ A P O と A P ′ O の相似 Step⑤ C O P と O ′ C P ′ の相似 Step⑥ (1), (2), (3) を解く 三角関数を用いた証明 中学全学年 最長の辺を斜辺と仮定して 三平方の定理が成立するか 計算して確認しましょう 三平方 三平方の定理 直角三角形 逆 このノートが参考になったら、著者をフォローをしませんか？ 気軽に新しいノートをチェックすることができます！

質問コーナー Discuss Scratch

交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー

 Excel 三角形の斜辺の長さ 高さ 底辺の長さを残りの2辺からする方法 まとめ三平方の定理ピタゴラスの定理を使えば直角三角形の辺の長さは大体わかる 三平方の定理で直角三角形の辺の長さを求める問題はどうだった 今日勉強した問題のパターンは4つだったな 超基本タイプ a 2 は「 a の二乗」といい、「 a × a ＝ a 2 」と表記します。 a 2 =b 2 c 2 の関係が成り立つのは、直角三角形だけです。 これだけでも不思議ですが、さらに不思議なことがあります。 それは「 a=bc 」にも「 a 3 =b 3 c 3 」にもならないことです。 3つの辺の長さを二乗しないと「調和」が取れない 三平方の定理を使って面積を求める方法は？ 問題を使って解説するよ！ 次の三角形の面積を求めましょう。 まず、底辺を6㎝とした場合の高さとなるような線を引きます。 すると、三角形が2つの直角三角形に分けることができますね。 そこから左に

感銘を受けた数学 三平方の定理の美しき証明たち 大人のための数学教室 和 Note

三平方の定理 ピタゴラスの定理

直角三角形の3辺の長さに関する a 2 b 2 =c 2 という関係はピタゴラスの定理（三平方の定理）と呼ばれます。 この定理はその名の通り古くから知られていますが、本当にピタゴラス(cBC570cBC500)が発見したかどうか確証があるわけではありません。三平方の定理とは 直角三角形のときに利用できる 辺の長さの関係式でしたね。 それを発展させて考えていくと 直角三角形だけでなく 鋭角、鈍角三角形を見分ける方法として活用することができます。 入試などでは、活用する機会は少ないと思います三平方の定理とは、直角三角形において 斜辺の長さの2乗は、他の辺の長さの2乗の和に等しくなる。 というものです。 文章だけでは、難しく見えますが 非常に単純な定理です。 このように 斜辺の2乗の数と 他の辺を2乗して足した数が等しくなるの

三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学

かみのドリル 三平方の定理

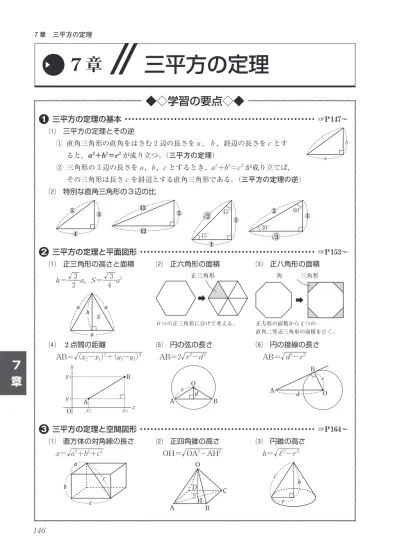
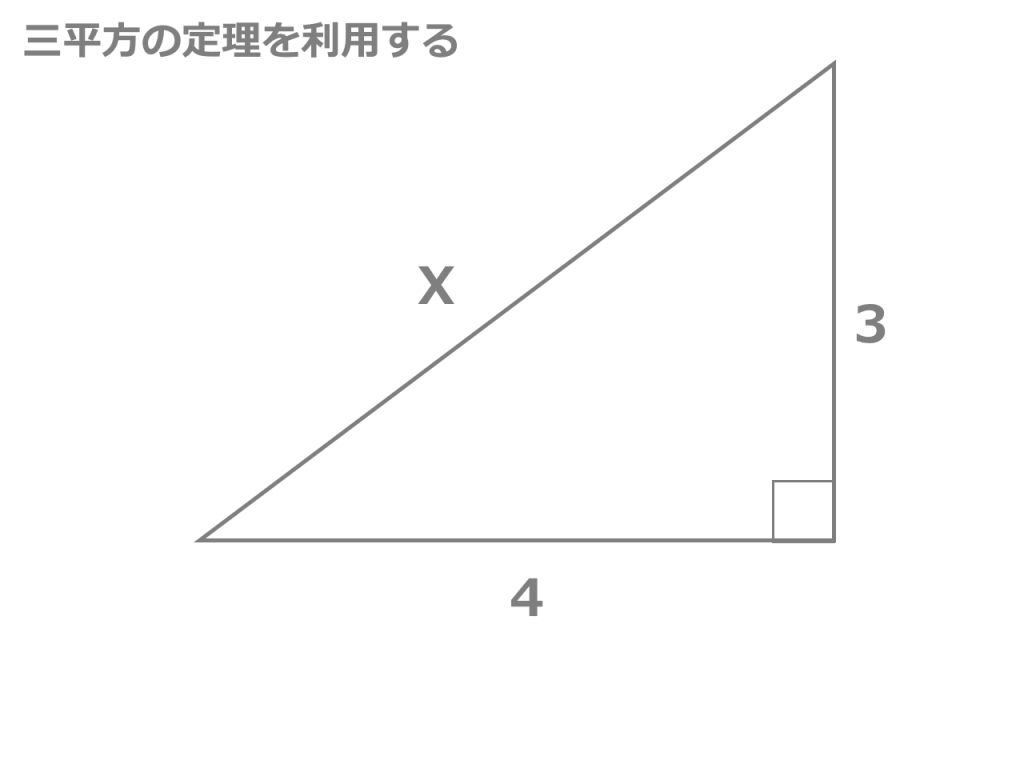
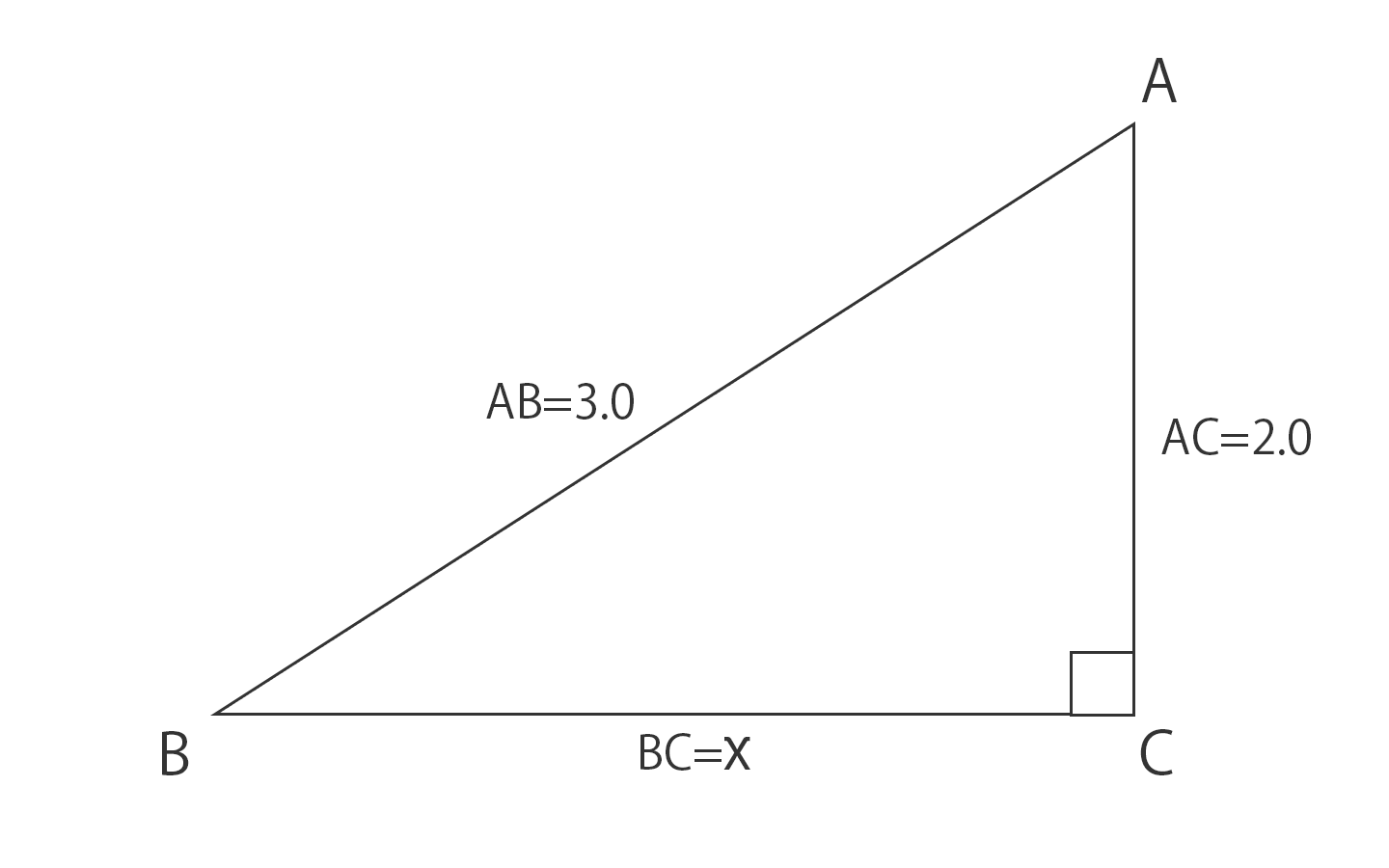
が成り立つとき，その三角形は直角三角形です． （これを三平方の定理の逆といいます．） 一番長い辺が斜辺です． ※ 直角三角形であるかどうかを調べるには， a 2 b 2 と c 2 を比較してみれば分かります． 例 三辺の長さが 3,4,5 の三角形が直角三角形中点連結定理 a b c m n abcの2辺ab, acの中点をそれぞれm, nとすると mn//bc, mn= 1 2 bcとなる。 定理の証明 amnと abcにおいて ∠aは共通(1) mはabの中点なのでamab=12 nはacの中点なのでanac=12 よってamab=anac=12(2)三平方の定理(基本問題1) 例題 次の直角三角形で、xの値を求める。 x 2 6 xが斜辺なので 2 2 6 2 = x 2 x 2 = 40 x = ±2 √ 10 x > 0より x =2 √ 10 x 4 5 斜辺が5なので x 2 4 2 =5 2 x 2 = 2516 x 2 =9 x=±3 x>0より x=3 次の直角三角形で、xの値をそれぞれ求めよ。

三平方の定理 自動計算サイト

1

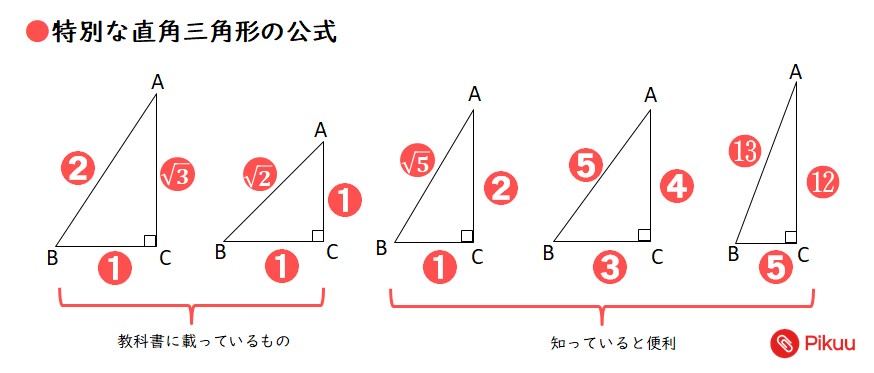
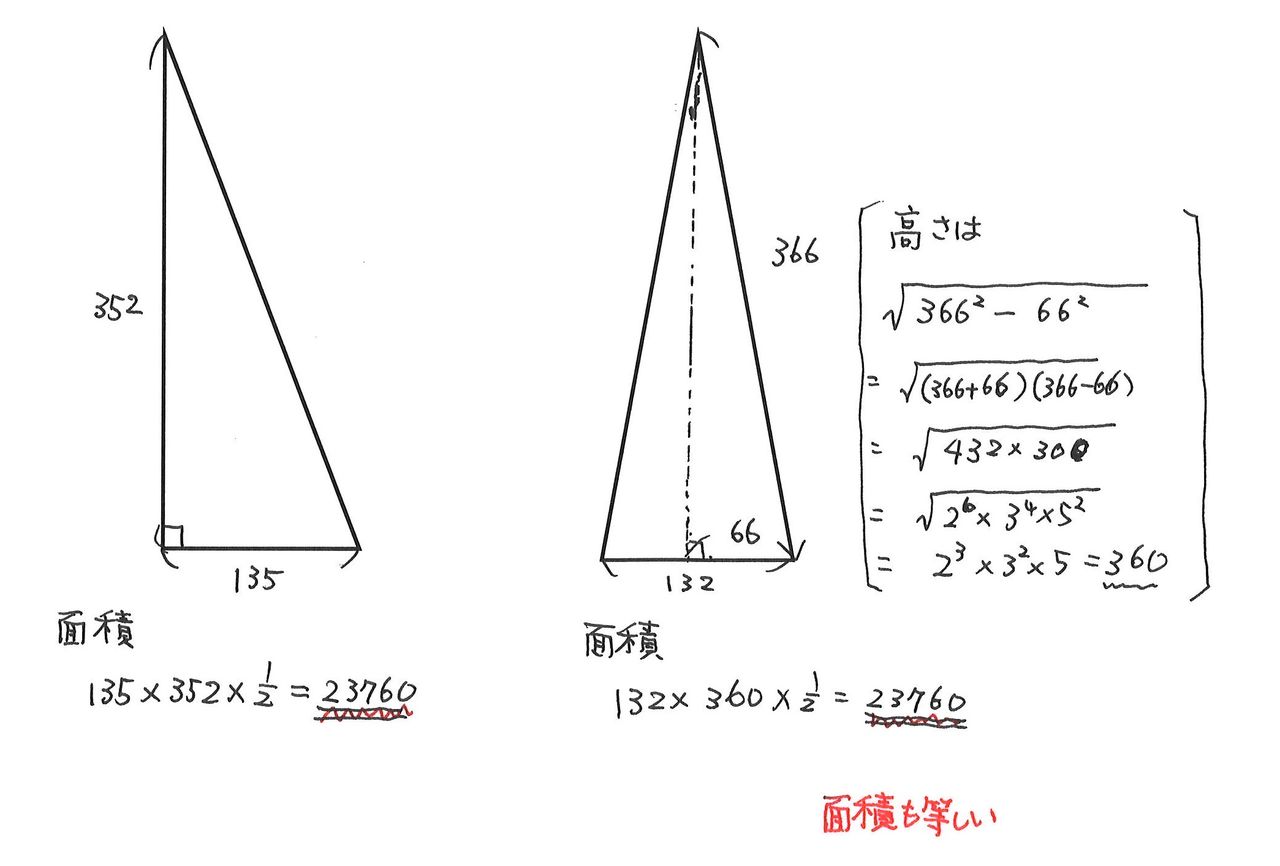
 中学受験ですので、三辺の 辺の比が整数となる直角三角形 がよく出題されます。 左側の $\textcolor{red}{345}$ の 三角形 は 超頻出 なので、覚えておいて欲しいですが、他の2つは そんなのもあるんだぁ~ 程度で良いかなぁ と 思います。

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

三平方の定理の証明と使い方

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

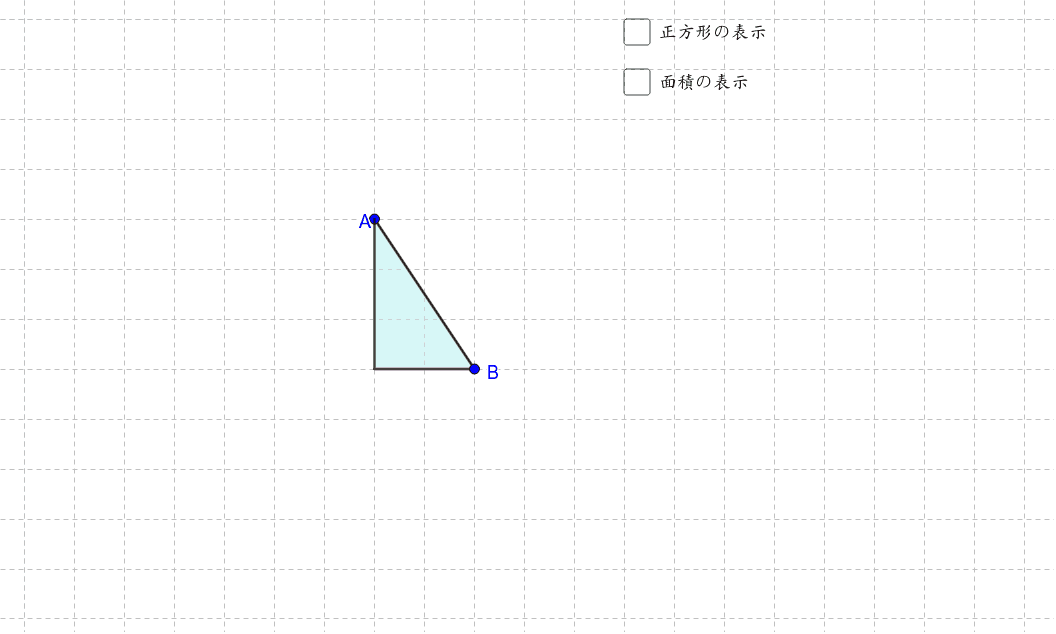
三平方の定理の導入 Geogebra

Python 三平方の定理 Unpyside

中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集 Waenavi

三平方の定理を英語で読んでみる

三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ１０選 遊ぶ数学

直角三角形の辺の長さ 合同条件 面積について アタリマエ

三平方の定理で辺を求める Youtube

三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者

3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ

三平方の定理を直角三角形二つで証明 Youtube

三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく

三平方の定理の証明 外接円と直角二等辺三角形を利用した証明 Fukusukeの数学めも

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

直角三角形ではない場合ピタゴラスの定理はどう使えるのでしょうか Quora

特別な直角三角形の辺の比 無料で使える中学学習プリント

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

三平方の定理 おやじさん ネット

円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト

三平方の定理の証明 相似を利用した証明１ Fukusukeの数学めも

1

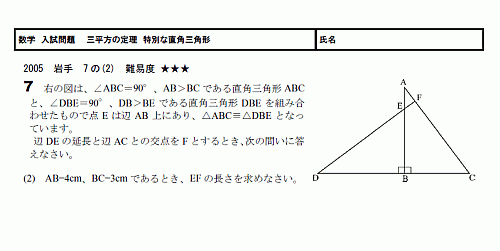
高校入試対策数学 特別な直角三角形を使った問題 Pikuu

中学数学 直角三角形3 4 5以外に知ってる

三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく

中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog

三平方の定理の公式とは 証明から計算問題まで紹介 辺の比と角度一覧表も テラコヤプラス By Ameba

Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集 Waenavi

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

三平方の定理

特別な直角三角形の３辺の比 の問題が分からないんですけど やり方を教えてく Clearnote

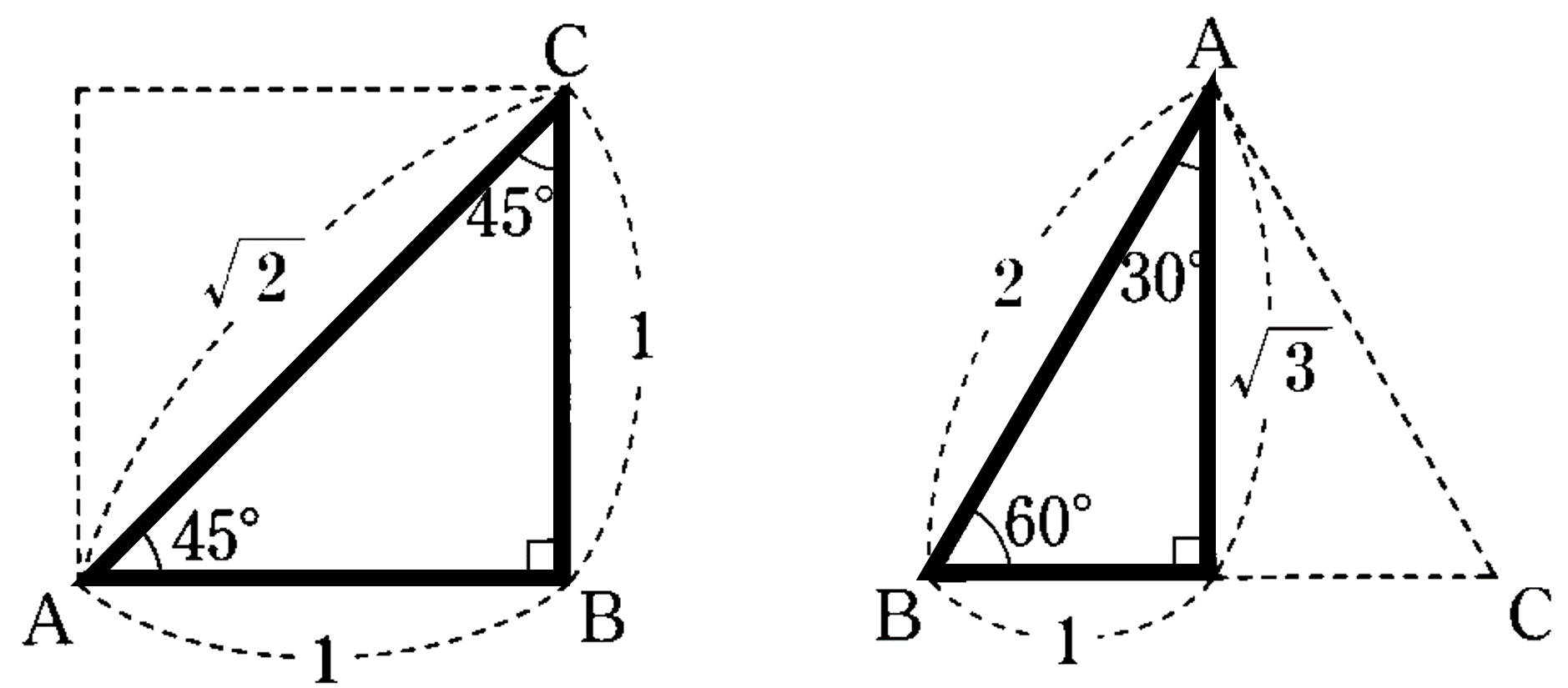
７章 三平方の定理 タカラゼミ

3

三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者

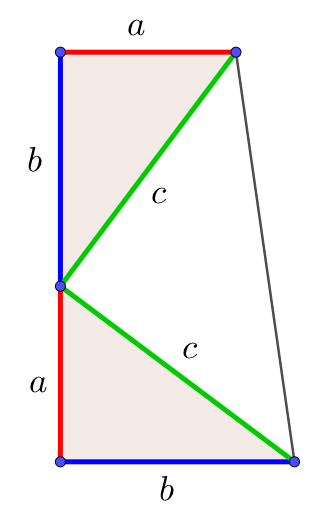
三平方の定理の証明３ 大統領の台形 キソカラ

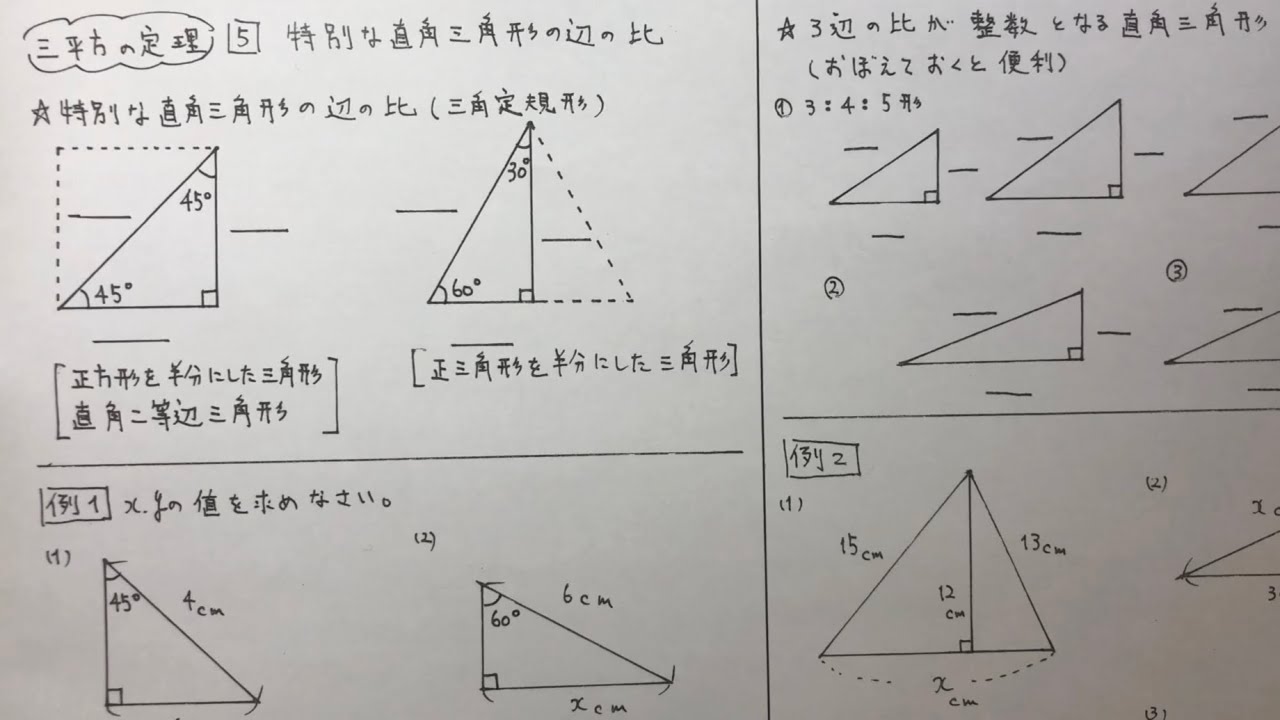
中3数学 三平方の定理5 特別な直角三角形の辺の比 Youtube

三平方の定理の公式とは 証明から計算問題まで紹介 辺の比と角度一覧表も テラコヤプラス By Ameba

三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者

数学 中3 61 三平方の定理 基本編 Youtube

高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月

三平方の定理 スタディーx

特別な直角三角形の3辺の比 三平方の定理 中学生からの勉強質問 数学 進研ゼミ中学講座

三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト

2つの直角三角形の角の和 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog

三角形のペア 大田 桐光本部校 ブログ

Ppt ６ 三平方の定理 Powerpoint Presentation Free Download Id

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

三平方の定理

三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典

三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導

三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学

โน ตของ 中学数学 三平方の定理のキホン ช น Junior Clearnote

Python 三平方の定理 Unpyside

三平方の定理について考える５ 直角三角形の合同条件のひとつ 身勝手な主張

三平方の定理 特別な直角三角形 イ弋マ本ゼミナール

三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学

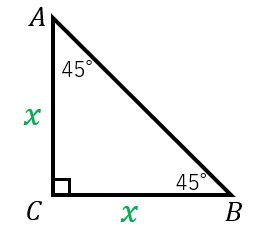
30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学

3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ

三平方の定理 覚えておきたい基本公式を解説 数スタ

三平方の定理の応用

中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ Youtube

三平方の定理の逆ってなに どうやって証明するの 数スタ

1

三平方の定理 特別な直角三角形の3辺の比 中学数学 定期テスト対策サイト

3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく

三平方の定理について考える４ 三角形の相似を使った証明方法 身勝手な主張

交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題

正方形を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト

三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく

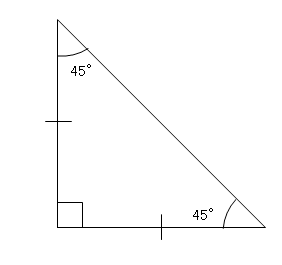
三平方の定理 特別な直角三角形 1 ネット塾

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

Mathematics 三平方の定理 ２ 特別な直角三角形 働きアリ

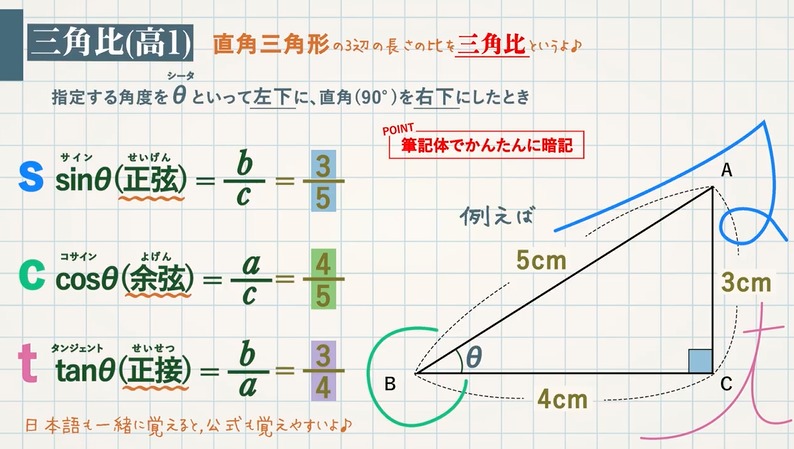
三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者

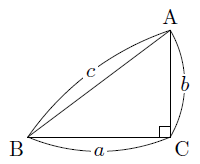
直角三角形の辺の長さ まなびの学園

三平方の定理およびその逆 証明 理数系無料オンライン学習 Kori

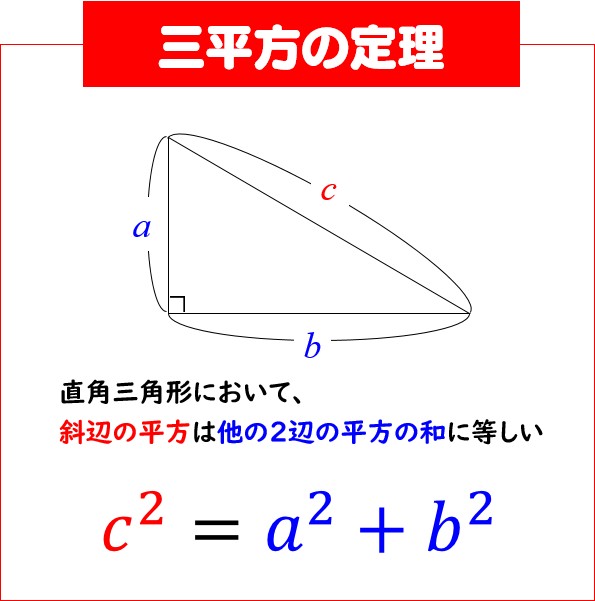
三平方の定理の証明 直感的に分かる図で解説します 数学fun

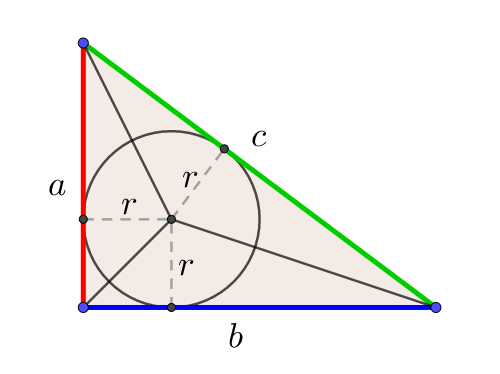
三平方の定理の証明４ 直角三角形と内接円 キソカラ

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

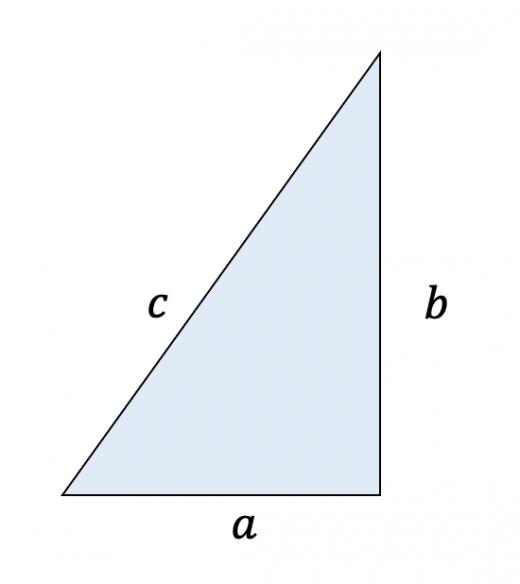
直角三角形の定義とさまざまな公式 高校数学の美しい物語

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube

無料 中３数学 基本解説 解答プリント 334 三平方の定理２ 比の利用

中学３年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生

三平方の定理の証明２ ４つ直角三角形と真ん中の四角 キソカラ

Incoming Term: 直角三角形 三平方の定理, 直角三角形 三平方の定理 覚え方, 直角三角形 三平方の定理 計算,